My original analysis was done pretty directly after the event.
I generated the following plot:

I presented a write-up here: https://www.reddit.com/r/TheSilphRoad/comments/9vdjix/analysing_dirty_data_why_i_believe_the_actual/
This early data got me a lot of negative replies as I assumed the issue was false data / players not deducting previously found Pokemon. So already in my first analysis did I propose a shiny rate of around 1 in 50 combined with a zero rate. Albeit the reason I assumed for the zero rate clearly was wrong.
I followed this up with a simulation. https://www.reddit.com/r/TheSilphRoad/comments/9vj648/simulation_results_how_two_drop_rates_1_in_50_and/

I’m still proud about this reddit article. It was my very first article that got me a platinum reddit medal (I didn’t even get a silver ahead of that).
But this model was hotly debated and I still remember clearly how some researchers I valued highly described my approach to the statistics in quite derogatory terms. I was told that the slope had no relationship to the actual shiny rate.
I never published the following graph:
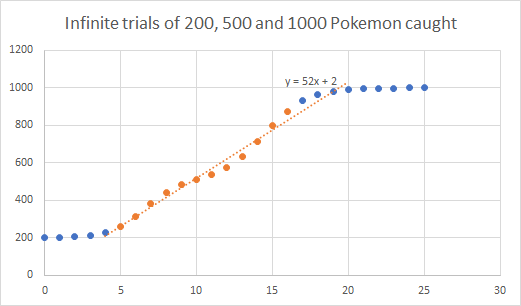
This graph is based on a binomial distribution and calculates how many Pokemon on average you have checked for a 1 in 50 shiny rate assuming you either checked exactly 200, 500 or 1000 Pokemon.
This graph is meaningless for values <4 and meaningless for values >20. But in between the slope pretty well describes exactly the drop rate. Therefore mathematically there is nothing wrong in plotting shiny found vs Pokemon observed. The slope will give you the shiny rate.
This even works if you have a random number x added to your total. It just shifts the graph upwards.
There is of course a reason that statisticians don’t do it this way round. You need a lot of data and it needs to be spread widely enough to be accurate. It is therefore not random that I early on found a rate of 1 in 50 intermixed with a zero rate- even if I lacked an explanation why.
Was I likely over interpreting my finding and underestimating the error involved.
I’m clearly guilty on that count. And I will leave it there.